Mở đầu bài viết này tôi muốn kể cho các bạn nghe một câu chuyện, về nhà Toán học Niccolo Fontana (1499-1557) sống tại công cuốc Venezia (nay là một thành phố của Italia) với biệt danh Tartaglia (kẻ nói lắp).
Tartaglia có một tuổi thơ đầy bất hạnh. Năm ông 13 tuổi quân Pháp tràn vào quê hương ông, cha ông (một người đưa thư) đã dắt ông chạy trốn vào nhà thờ cùng với mọi người trong làng. Không may họ đã bị phát hiện và cuộc thảm sát diễn ra ngày trong nhà thờ ấy: Cha ông bị giết chết, Tartaglia bị chém ngang mặt cắt đứt miệng và lưỡi…Người mẹ trong những nỗ lực cuối cùng đã tìm thấy đứa con trai và người chồng đã chết của mình. Chẳng thể có tiền lo thuốc thang điều trị cho đứa con trai, bà nhớ lại rằng những con chó khi bị thương thường hay liếm vào vết thương, và thật thần kì với cách chạy chữa đặc biệt đó mà vết thương của Tartaglia đã bình phục. Mẹ ông chỉ gom góp đủ tiền để ông được đi học trong 15 ngày và chỉ trong quãng thời gian ngắn ngủi đó Tartaglia đã tìm cách trộm được một cuốn vở đánh vần và tự học cách đọc và viết. Tartaglia với vòm miệng bị hỏng nói năng rất khó khăn và một cuộc sống nghèo khổ đã tự học thành tài và được rất nhiều người kính phục.
Tartaglia bị vướng vào một cuộc thách đấu Toán học giải các phương trình bậc 3 khác nhau với nhóm môn đệ của Del Ferro (nhà Toán học đã tìm ra cách giải một lớp phương trình bậc 3 đặc biệt). Bởi vì đến thời điểm ấy vẫn chưa có ai tìm ra được cách giải phương trình bậc 3 tổng quát nên cuộc thách đấu đã được sự quan tâm của cả giới Toán học Châu âu thời bấy giờ. Cảm thấy hơi nao núng vì đối thủ quá tự tin, Tartaglia đã miệt mài suy nghĩ và trước kì thi 8 ngày ông đã tìm ra được cách giải tổng quát.
Vào ngày 22-2-1535, các nhà toán học và những người hâm mộ ở nhiều nước châu Âu kéo về thành phố Milan để dự cuộc thi tài. Mỗi bên sẽ ra cho đối phương 30 phương trình bậc 3 khác nhau và giải trong 2h. Và bởi vì nhóm Ferro chỉ giải được một lớp các phương trình bậc 3 đặc biệt trong khi Tartaglia nắm giữ trong tay “Cửu âm chân kinh” do ông sáng tạo ra nên không có gì bất ngờ khi tỉ số trận quyết đấu là 30:0. Tartaglia trở nên rất nổi tiếng khắp Châu Âu sau thành công vang dội này, dù vậy ông vẫn giữ kín bí mật về cách giải của mình.
Lại nói về Cardano, một bác sĩ yêu Toán, ông cũng đã nghiên cứu về đề tài này nhiều năm mà chưa có kết quả. Cardano đã nhiều lần thuyết phục Tartaglia chia sẻ bí mật đó và đã được Tartaglia chấp thuận với một lời tuyên thệ sẽ không tiết lộ cho bất kì ai. Tuy vậy, Cardano đã nuốt lời. Ông đã công bố cách giải này trong một cuốn sách của mình và mặc dù trong lời nói đầu của cuốn sách ông có xác nhận rằng cách giải này là của Tartaglia, giới Toán học dường như vẫn chỉ nhớ đến ông khi nhắc đến phát minh này.
Cũng dễ hiểu là Tartaglia đã bị tổn thương như thế nào, một cuộc tranh luận lớn nổ ra, và cũng như lần trước Tartaglia gửi đến một lời thách đấu. Không may cho Tartaglia, lần này ông đã không ngờ rằng Lodovico Ferrari, một học trò tài ba của Cardano từ phương pháp được thầy mình truyền lại đã tìm ra được cách giải tổng quát cho phương trình bậc 4. Và vì vậy, trong cuộc tranh luận đó Tartaglia đã thất bại cay đắng và mang nỗi uất hận trong lòng cho đến khi ông mất…
Trên phương diện một người bạn, Cardano đã hành xử không đúng. Nhưng không thể phủ nhận rằng, việc công bố rộng rãi phát minh này đã giúp ích rất nhiều cho sự phát triển của Toán học. Lịch sử sẽ mãi vẫn là lịch sử, đúng hay sai đôi khi chỉ là tương đối. Những hậu bối chúng ta hôm nay sẽ cùng tìm hiểu phát minh trọng đại này để rồi từ đó các bạn sẽ thấy một thành viên mới của gia đình nhà số: số phức, đã xuất hiện kì ảo như thế nào.
Tôi từng kể cho nhiều em học sinh nghe về cuộc hành trình tìm ra số phức, câu chuyện về phương pháp giải phương trình bậc 3 và hầu hết các em đều muốn hiểu rõ về phát minh quan trọng này. Đó cũng là lý do tôi viết bài viết này và sẽ trình bày sau đây về phương pháp giải phương trình bậc 3 của Tartaglia:
Xét phương trình bậc 3 có dạng: 
Ta tìm cách đưa phương trình (1) này về dạng khuyết 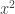 .
.
Muốn vậy ta thực hiện phép đổi biến: . Thay vào (1) ta được:
. Thay vào (1) ta được: 
Bằng cách đặt: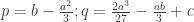 . Ta đưa (1) về phương trình sau (khuyết số hạng bậc 2):
. Ta đưa (1) về phương trình sau (khuyết số hạng bậc 2):  (2)
(2)
Muốn vậy ta thực hiện phép đổi biến:
Bằng cách đặt:
Nhiều bạn sẽ hỏi tại sao biết cách đổi biến như vậy? Thật ra cũng đơn giản ban đầu vì bạn chưa biết nên đặt thế nào, bạn hãy cứ tạm đặt là 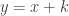 . Sau đó hãy cứ rút x và thế vào phương trình (1) để được một phương trình bậc 3 mới theo y. Đối với phương trình này ta sẽ để cho hệ số của
. Sau đó hãy cứ rút x và thế vào phương trình (1) để được một phương trình bậc 3 mới theo y. Đối với phương trình này ta sẽ để cho hệ số của 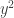 phải bằng 0. Từ đó mà biết được phải chọn k bằng bao nhiêu.
phải bằng 0. Từ đó mà biết được phải chọn k bằng bao nhiêu.
Để giải quyết phương trình (2) này, Tartaglia thực hiện thêm một lần đổi biến nữa. Ông đặt 
Trong đó u, v là 2 ẩn mới. Các bạn có thể nghĩ rằng sao ta không đặt giống hồi nãy để làm mất luôn hạng tử bậc nhất của (2). Rất tiếc là mưu đồ này chắc chắn sẽ thất bại vì nói chung khi đổi biến thích hợp để mất hạng tử bậc nhất thì nó lại “mọc” ra hạng tử bậc 2 ban đầu. Bây giờ là lúc các bạn phải thật chú ý, việc đặt y=u+v thì u và v hoàn toàn có quyền được “ràng buộc” với nhau theo một cách tùy ý nào đó. Quyền chọn lựa ràng buộc này ta sẽ chọn lựa sau. Còn bây giờ ta sẽ chuyển phương trình (2) về dạng mới theo u, v:
Trong đó u, v là 2 ẩn mới. Các bạn có thể nghĩ rằng sao ta không đặt giống hồi nãy để làm mất luôn hạng tử bậc nhất của (2). Rất tiếc là mưu đồ này chắc chắn sẽ thất bại vì nói chung khi đổi biến thích hợp để mất hạng tử bậc nhất thì nó lại “mọc” ra hạng tử bậc 2 ban đầu. Bây giờ là lúc các bạn phải thật chú ý, việc đặt y=u+v thì u và v hoàn toàn có quyền được “ràng buộc” với nhau theo một cách tùy ý nào đó. Quyền chọn lựa ràng buộc này ta sẽ chọn lựa sau. Còn bây giờ ta sẽ chuyển phương trình (2) về dạng mới theo u, v:
Để cho phương trình trở nên đơn giản hơn, ở đây ta sẽ sử dụng quyền ràng buộc của mình, cụ thể ta sẽ cho 
Lúc đó (2) trở thành: 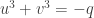 . Tóm lại u, v thõa 2 điều kiện sau:
. Tóm lại u, v thõa 2 điều kiện sau:
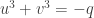 và
và 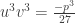
Suy ra 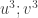 là 2 nghiệm của phương trình:
là 2 nghiệm của phương trình: 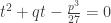 (3)
(3)
Từ đó mà tìm được u,v tiếp theo là tìm y và cuối cùng là tìm được nghiệm x.
Từ đó mà tìm được u,v tiếp theo là tìm y và cuối cùng là tìm được nghiệm x.
Cũng không quá khó hiểu phải không các bạn. Phương trình bậc ba với các phép đổi biến thích hợp đã được đưa về một phương trình bậc hai (phương trình (3)). Tuy vậy phương pháp tuyệt vời này lại có một điểm yếu chết người, và tôi sẽ chỉ ra điểm yếu này qua ví dụ sau đây:
Xét một phương trình bậc ba đơn giản mà chúng ta đã biết chắc chắn được 3 nghiệm của nó: 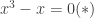 . Phương trình (*) rõ ràng là có 3 nghiệm 0,-1,1. Bây giờ ta sẽ áp dụng phương pháp của Tartaglia để giải quyết nó. Vì phương trình đã ở dạng khuyết số hạng bậc 2 nên ta sẽ đặt luôn
. Phương trình (*) rõ ràng là có 3 nghiệm 0,-1,1. Bây giờ ta sẽ áp dụng phương pháp của Tartaglia để giải quyết nó. Vì phương trình đã ở dạng khuyết số hạng bậc 2 nên ta sẽ đặt luôn 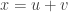
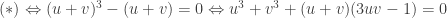
Tất nhiên là ta sẽ chọn u,v thõa: . Lúc này
. Lúc này 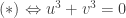 . Theo trên thì
. Theo trên thì 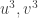 là nghiệm của phương trình:
là nghiệm của phương trình:
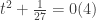
Tất nhiên là ta sẽ chọn u,v thõa:
Oái ăm thay phương trình (4) này lại vô nghiệm! Vậy 3 nghiệm ban đầu của mình đã đi đâu mất? Điểm yếu của phương pháp này ở chỗ: Không phải bao giờ cũng tìm được 2 số u, v mà 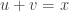 và
và  . Trong trường hợp ta vừa xét ở trên, các bạn cũng nhận thấy là không thể tìm được u,v nào thõa chẳng hạn
. Trong trường hợp ta vừa xét ở trên, các bạn cũng nhận thấy là không thể tìm được u,v nào thõa chẳng hạn 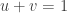 và
và  .
.
Đứng trước khó khăn này các vị tiền bối của chúng ta có 2 sự lựa chọn. Một là từ bỏ phương pháp hấp dẫn này, còn sự lựa chọn thứ 2 mới nghe tưởng chừng rất liều lĩnh và điên rồ: Chấp nhận có căn bậc 2 của số âm để giải tiếp phương trình 6 tìm u,v. Một ý định điên rồ nhưng đầy tham vọng. Nào chúng ta sẽ thử:
Chúng ta cứ xem là có căn bậc hai của số âm, nói riêng là căn bậc hai của -1 và đặt nó là i:  và
và 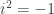 . Lúc này ta có thể giải tiếp phương trình (4):
. Lúc này ta có thể giải tiếp phương trình (4): 
Phương trình này có 2 nghiệm là 
Để tìm được u và v vấn đề là phải tìm được căn bậc ba của i. Có 3 căn bậc ba như vậy, lần lượt là:
Trở lại vấn đề, chúng ta tìm được 3 giá trị của u là:
 ;
;  ; và
; và 
3 giá trị của v lần lượt là:
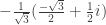 ;
;  ; và
; và 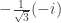
3 giá trị của v lần lượt là:
Các bạn có để ý là tôi đã sắp xếp lại các giá trị của v theo một thứ tự khác với u vì để cho tích các giá trị tương ứng của u và v là 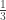 theo như ràng buộc ban đầu.
theo như ràng buộc ban đầu.
Bây giờ là lúc gặt hái thành quả, hãy xem ba giá trị của x tìm được sẽ là:
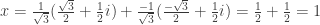
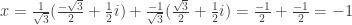
Và nghiệm thứ 3:
Và nghiệm thứ 3:
Thật không thể tin nổi, 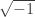 mà chúng ta liều lĩnh chấp nhận xuất hiện như một phép màu giúp ta vượt qua khó khăn bước tiếp theo con đường Tartaglia đã tìm ra để rồi sau đó nó biến mất để lại cho chúng ta 3 nghiệm thực mà chúng ta đã biết từ ban đầu.
mà chúng ta liều lĩnh chấp nhận xuất hiện như một phép màu giúp ta vượt qua khó khăn bước tiếp theo con đường Tartaglia đã tìm ra để rồi sau đó nó biến mất để lại cho chúng ta 3 nghiệm thực mà chúng ta đã biết từ ban đầu. 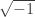 rõ ràng là không có thực, bởi thế mà người ta gọi nó là “ảo” (chính xác hơn: đơn vị ảo) nhưng nó xuất hiện cứ như một phép màu của ông Bụt vậy, chỉ khác một điều là chúng ta không chấp nhận để nó biến mất mãi mãi. Chúng ta níu giữ nó lại nghiên cứu để hiểu hơn về phép màu kì ảo này, phát triển lý thuyết về nó để rồi bây giờ số phức (những số có dạng a+bi) đã tự hào là một thành viên quan trọng trong đại gia đình nhà số và góp phần tạo nên bước phát triển mới trong bảng vàng lịch sử của Toán học.
rõ ràng là không có thực, bởi thế mà người ta gọi nó là “ảo” (chính xác hơn: đơn vị ảo) nhưng nó xuất hiện cứ như một phép màu của ông Bụt vậy, chỉ khác một điều là chúng ta không chấp nhận để nó biến mất mãi mãi. Chúng ta níu giữ nó lại nghiên cứu để hiểu hơn về phép màu kì ảo này, phát triển lý thuyết về nó để rồi bây giờ số phức (những số có dạng a+bi) đã tự hào là một thành viên quan trọng trong đại gia đình nhà số và góp phần tạo nên bước phát triển mới trong bảng vàng lịch sử của Toán học.
Ps: Xin tỏ lòng biết ơn với Giáo sư Nguyễn Cảnh Toàn về bài viết: “Số ảo ngu ngốc hay thông minh” đăng trên báo Toán học tuổi trẻ. Bài viết đã tạo nguồn cảm hứng cho việc học toán của tôi và cũng chính là nguồn tham khảo chính cho bài viết này.
Nguồn https://toanhoctuoidep.wordpress.com



0 nhận xét:
Đăng nhận xét
Xin mời bạn cho một nhận xét để động viên người viết.
(Nhận xét của bạn sẽ được kiểm duyệt trước khi đăng)